소리의 파동 푸리에 변환
우리 생활에서 음악이나
소리가 주는 영향력은 매우 큽니다.

음악 소리 뿐만 아니라 모든 소리는
파동으로 이뤄져 있고, 이런 파동을
정보통신 장치로 빠르게
주고 받는 데는 푸리에 변환
이라는 기술이 큰 몫을 합니다.

푸리에는 62세 되던 1830년 사망한
프랑스 수학자이자 물리학자로
푸리에 변환의 원리를 고안하고 증명했어요.
그의 기술을 적용한
아아디어 중에는 사람들을
깜짝 놀라게 하는 것이 많습니다.
푸리에 변환을 응용한 첨단 사례가
발에 챌 정도로 많아요.
첨단기술에 대한 더 나은 시야를
갖기 위해 푸리에 변환을 이해해봅시다.
푸리에 변환의 기본 아이디어는
모든 파동의 모양을
진동수가 다른 단순한 파동들의
합으로 나타낼 수 있다는 것이죠.
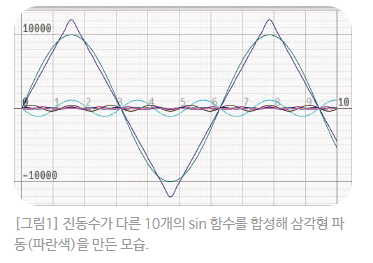
첫번째 그림을 통해
이것을 전형적으로 설명할
수 있어요. 이 그림은 진동 주기가
다른 sin 함수 10개를 진폭이
다르게 합성한 결과입니다.
부드러운 sin 함수들을 합성해 전혀
다른 모양인 삼각형 파동을 만들었어요.
다음은 그림2의 원리를
기술자들이 어떻게 응용하는지 설명하기
위한 것입니다.
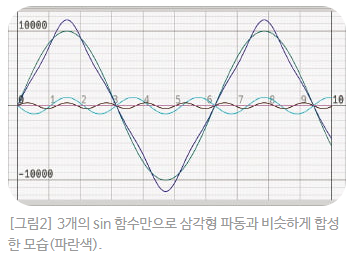
[그림2]는 [그림1]에서 언급한 10개의
sin 파동 중 진폭이 제일 큰 3개만으로
합성한 결과입니다.
첫번째 그림의 삼각형 파동과
똑같진 않아도 비슷한 모양의
파형을 얻을 수 있어요.
푸리에 변환을 수학적으로
증명할 때는 무한히 많은 sin파동을
합하면 원하는 파형을 만들 수 있다는
내용이었지만, 기술자들은 그 중
몇개의 sin 파동만으로 비슷한
파형을 만들 수 있다는 데서 착안해
다양한 응용 사례를 만들고 있어요!
푸리에 변환의 가장 흔한
응용 사례로는 정보 압축 기술이 있어요.

휴대용 전화기는 배터리를 많이
사용하지 않기 위해
목소리의 핵심 요소만 송신하고,
이런 신호를 받으면 원래
목소리와 비슷한 목소리로 합성해주죠.
그래서 전화기 목소리는
원래 목소리와 조금 다른 느낌이 들어요.

음질이 중요한 음악을 저장할 때는
귀가 예민한 사람만 느낄 수 있는
진동수의 sin 파동을 모두 제거해
50mb 크기의 음악 파일을 5mb수준으로
압축해 저장할 수 있어요.
이때 사용하는 기술을 보통
'mp3'라고 부릅니다!

보통의 사람에게 푸리에 변환 얘기는
낯설겠지만
모든 파동의 모양은 진동수가
다른 단순한 파동들의 합으로
나타낼 수 있다는 것입니다!
출처
'정수학 전문학원의 수학공부 > 기초부터 차근차근' 카테고리의 다른 글
| 2023 3월 학력평가 고1 · 고2 매우 중요한 시험 꿀 팁! (0) | 2023.03.20 |
|---|---|
| 고1 순열의 의미를 알고 계산해요 (0) | 2023.03.17 |
| 2024 사회/ 과학탐구 영역 과목 선택 법 (0) | 2023.03.13 |
| 초등학생 신학기 수학공부 시작이 중요해요 (1) | 2023.03.10 |
| 실수도 실력이라는 말 수학 잘못된 습관 고치기 (0) | 2023.03.08 |








